Introduction
I love ‘Concurrency in Practice’. Its a Java concurrency book written by Brian Goetz, Doug Lea and Joshua Bloch. It is considered a definitive guide on the subject. These fine folks were also involved in JSR166 and have authored many of the concurrency/collection classes in JDK. It is fascinating to walk through their code. There is lot to learn about code structure, performance, trade-offs etc.
Let’s start with HashMap and its cousin LinkedHashMap.
Basics
If you want to understand how HashMaps are typically implemented at basic level, I highly recommend this video explaining Go’s HashMap
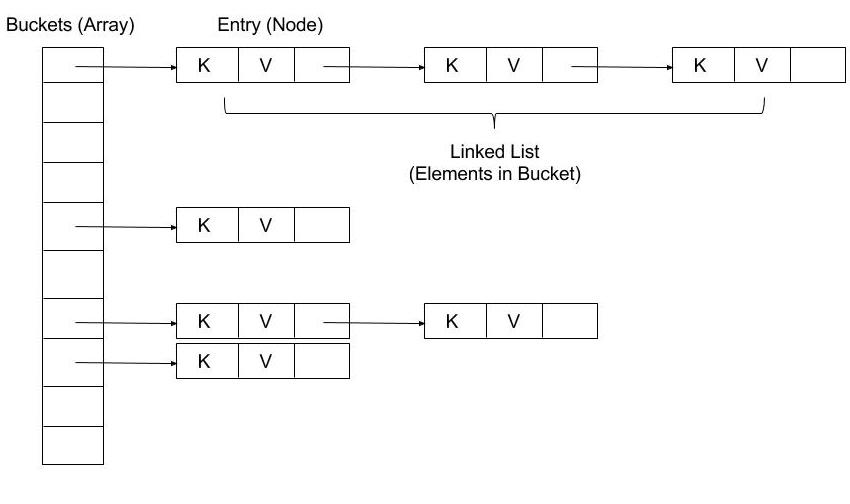
In short, HashMap is backed by an array. During put operation, hashcode of key is calculated, and Entry (key+value) is inserted in array (based on hashcode % array’s size). If more keys are added with same hashcode, linkedlist is formed with previously added keys.
Let’s focus on the interesting parts of the class (whole code here: HashMap & LinkedHashMap)
Initialization
- If the initial capacity and load-factors are not provided, they default to 16 and 0.75 respectively.
- Closest factor of 2 If initial capacity is given, it is increased to the closest factor of 2 by using this bit twiddling algorithm.
- Why factor of 2: When table is resized (doubled), the elements in linked list can easily be assigned to new indexes without performing modulo operation. This is awesome! Eg: If hash=9, oldTableSize=8, oldIndex=1 (9%8), newTableSize=16, newIndex=9 (9%16) = oldTableSize + oldIndex
- Table not initialized yet: Interesting that the array (variable table) is not initialized in constructor. So no memory allocated yet.
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16
static final int MAXIMUM_CAPACITY = 1 << 30;
static final float DEFAULT_LOAD_FACTOR = 0.75f;
public HashMap() {
this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
}
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
this.loadFactor = loadFactor;
this.threshold = tableSizeFor(initialCapacity);
}
static final int tableSizeFor(int cap) {
int n = cap - 1;
n |= n >>> 1;
n |= n >>> 2;
n |= n >>> 4;
n |= n >>> 8;
n |= n >>> 16;
return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}
Linked-Lists vs Trees
If there are multiple elements with same hashcode, they are linked to each other forming linked-list (also called as Bins). Starting with Java 8 as part this JEP, if number of elements with same hashcode crosses certain threshold, the list is converted to a balanced Red-Black tree.
Red-Black tree is a sorted tree, in which search takes max log(n) operations. Though, for the sorting to work, all the keys need to be comparable to each other (i.e. they need to implement Comparable interface).
If keys are not comparable then ofcourse it will be a tree with each node with only 1 child. This consumes twice the space is generally twice as slow.
Hashcode
-
Best Case: O(1). Hashcode of all the keys are distinct, then get and put operations run in O(1) i.e. constant time (independent of the number of keys in the map).
-
Worst Case (Bins): O(n). Hashcodes of all keys are same then same operations can take O(n) time (n = number of keys in the map).
-
Worst Case (Trees): O(log(n)). Hashcodes of all keys are same then same operations can take O(log(n)) time (n = number of keys in the map).
Note: Technically hashcode % table-length need to be distinct, because even distinct hashcodes can end up in same bin/tree i.e. collide.
String class: Special hash function and a new private field hash32 (to cache the hashcode) was added to String class in Java 7 to to use more complex hashing to generate unique hashes. This was specifically to improve performance in HashMaps (all variants). After implementing Trees instead of Bins (see section below), the field was removed since now the worst case operations take O(log(n)) instead of O(n).
Probability of list of size k
Unless there are programming mistakes or malicious code, hashcodes generally follow poisson distribution
In layman terms, typical keys inserted in the HashMap have hashcodes which are generally unique. The probability of 2 elements having same hashcode is low, 3 of them having same is even lower, and 8 elements having same hashcode is extremely rare (1 in 10 million).
Thus probability of having to create trees is very low (although, if you use custom class as key, and its hashcode is badly written then its still very much probable).
Code for computing hash
So in addition to the hashcode that we write for our keys, hashcode itself is (bitwise) shifted. This because some values with same lower bits can increase probability of same hashcodes.
/**
* Computes key.hashCode() and spreads (XORs) higher bits of hash
* to lower. Because the table uses power-of-two masking, sets of
* hashes that vary only in bits above the current mask will
* always collide. (Among known examples are sets of Float keys
* holding consecutive whole numbers in small tables.) So we
* apply a transform that spreads the impact of higher bits
* downward. There is a tradeoff between speed, utility, and
* quality of bit-spreading. Because many common sets of hashes
* are already reasonably distributed (so don't benefit from
* spreading), and because we use trees to handle large sets of
* collisions in bins, we just XOR some shifted bits in the
* cheapest possible way to reduce systematic lossage, as well as
* to incorporate impact of the highest bits that would otherwise
* never be used in index calculations because of table bounds.
*/
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}Example of such floats:
binary values of 2.0f, 18.0f and 215.0f all have same lower bits.
System.out.println(Long.toBinaryString(Float.floatToRawIntBits(2.0f)));
System.out.println(Long.toBinaryString(Float.floatToRawIntBits(18.0f)));
System.out.println(Long.toBinaryString(Float.floatToRawIntBits(215.0f)));
1000000000000000000000000000000
1000001100100000000000000000000
1000011010101110000000000000000Put Key-Value
- Lets skip hash function for now.
- (n - 1) & hash is same as hash % n, who knew!
- Code comments inline
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
// 1. Create table here by calling resize()
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
// 2. Find table index based on hash, if that table entry is empty, create new node and add
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
// 3. If table entry exists, then need to append (either to linked-list or the tree)
else {
Node<K,V> e; K k;
// 4. If first element in the table is same as new element to be added, get the element in e.
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
// 5. Above: Performance: Comparing int hash which is faster, if same then only call equals
e = p;
// 6. If this list is already converted to tree, add to element to the tree
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
// 7. Else add to the linked list
else {
for (int binCount = 0; ; ++binCount) {
// 8. Traverse the list until the end (one element at a time)
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
// 9. If elements in linked list are more than threshold, convert to tree
if (binCount >= TREEIFY_THRESHOLD - 1)
treeifyBin(tab, hash);
break;
}
// 10. If while traversing, any element equals and element-to-add then, get element in e
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
// 11. If element already exists
if (e != null) {
V oldValue = e.value;
// 12. Update with new value and return old value.
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
// 13. Increase modificationCount and Size
++modCount;
// 14. If after adding element, threshold is reached, increase table size.
if (++size > threshold)
resize();
// 15. Callback used for linkedhashmap not this regular hashmap
afterNodeInsertion(evict);
return null;
}Tree
- A linked list is converted to Red-Black tree only if list’s size exceeds threshold (8) and table size is greater than threshold (64).
- Code comments inline
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
// 1. If table size is less than MIN_TREEIFY_CAPACITY(64), then
// instead of creating tree, resize the table.
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize();
// 2. Convert linked list to tree
else if ((e = tab[index = (n - 1) & hash]) != null) {
TreeNode<K,V> hd = null, tl = null;
do {
// 3. create TreeNode for each element, and link using just prev/next
TreeNode<K,V> p = replacementTreeNode(e, null);
if (tl == null)
hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
// 4. Convert list of TreeNodes with prev/next to tree
if ((tab[index] = hd) != null)
hd.treeify(tab);
}
}
// 5. Method from within TreeNode class.
final void treeify(Node<K,V>[] tab) {
TreeNode<K,V> root = null;
for (TreeNode<K,V> x = this, next; x != null; x = next) {
next = (TreeNode<K,V>)x.next;
x.left = x.right = null;
// 6. For root i.e. first element
if (root == null) {
x.parent = null;
x.red = false;
root = x;
}
// 7. For all other TreeNodes
else {
K k = x.key;
int h = x.hash;
Class<?> kc = null;
for (TreeNode<K,V> p = root;;) {
int dir, ph;
K pk = p.key;
// 8. Sort to left or right, by comparing hash values
// 9. Imp: All elements of this tree have same (hash % table-size) values, but their
// actual hashes are different
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
// 10. If by chance 2 elements have exact same hash, then break tie using System.identityHashCode
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0)
dir = tieBreakOrder(k, pk);
// 11. Traverse TreeNode until appropriate (left/right) null child is found
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
// 12. Attach TreeNode as appropriate (left/right) child
x.parent = xp;
if (dir <= 0)
xp.left = x;
else
xp.right = x;
// 13. Tree can become unbalanced after addition of TreeNode, rebalance
// The root can change during balancing, re-assign to root
root = balanceInsertion(root, x);
break;
}
}
}
}
// 14. If during balancing root node changed, then table[hash % size] != root,
// fix this by change table's index to root
moveRootToFront(tab, root);
}
// 15. Called when number of elements in tree are less than threshold
final Node<K,V> untreeify(HashMap<K,V> map) {
Node<K,V> hd = null, tl = null;
for (Node<K,V> q = this; q != null; q = q.next) {
Node<K,V> p = map.replacementNode(q, null);
if (tl == null)
hd = p;
else
tl.next = p;
tl = p;
}
return hd;
}
Get value from key
Not much to see here. Straight forward code.
- If its a list traverse till the end (if its a tree, traverse the tree).
- Code comments inline.
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
// 1. Validate table not null, and hash table entry is not null
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
// 2. Check first element, for performance,
// since in most cases, where hashcodes are unique, there will be only 1 element
if (first.hash == hash &&
((k = first.key) == key || (key != null && key.equals(k))))
return first;
// 3. If there are more elements, traverse tree or linked-list accordingly
if ((e = first.next) != null) {
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}
final TreeNode<K,V> getTreeNode(int h, Object k) {
return ((parent != null) ? root() : this).find(h, k, null);
}
// Method within TreeNode class
final TreeNode<K,V> find(int h, Object k, Class<?> kc) {
TreeNode<K,V> p = this;
do {
int ph, dir; K pk;
TreeNode<K,V> pl = p.left, pr = p.right, q;
// 4. If node's hash greater than h, store left child tree in p
if ((ph = p.hash) > h)
p = pl;
// 5. If node's hash less than h, store right child tree in p
else if (ph < h)
p = pr;
// 6. If node's hash and key match, then return the node
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
// 7. If left child tree is null, then store right child tree in p
else if (pl == null)
p = pr;
// 8. If left child tree is null, then store right child tree in p
else if (pr == null)
p = pl;
// 9. If keys are comparable, compare and decide left or right child tree
else if ((kc != null ||
(kc = comparableClassFor(k)) != null) &&
(dir = compareComparables(kc, k, pk)) != 0)
p = (dir < 0) ? pl : pr;
// 10. Search recursively in right tree first.
else if ((q = pr.find(h, k, kc)) != null)
return q;
// 11. Set p as left child tree, and let while loop recursively search with p
else
p = pl;
} while (p != null);
return null;
}
Resizing table
- Used for both resizing and initializing table for first time.
- Code Comments inline
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
// 1. Validate less than MAX
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
// 2. Double capacity and threshold
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
// 3. Create table
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
// 4. Loop through old table to reassign all elements
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
// 5. Just assign for single element
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
// 6. Split the tree in 2 if a TreeNode
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
// 7. Split the linked list
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
// 8. Take advantage of factor of 2 size of table
// Either new index of element will be the same, or oldTableSize + oldIndex
// Assign to appropriate list
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
// 9. Attach list to appropriate table indexes
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}LinkedHashMap
- Its Node extends HashMap node and adds before, after Entry references to keep track of insertion order.
- Note that these new references form a doubly linked list, and is completely unrelated to the HashMap’s list, which keeps track of all elements with same hashcode.
- Code comments inline
// 1. Extra references to keep track of insertion order.
static class Entry<K,V> extends HashMap.Node<K,V> {
Entry<K,V> before, after;
Entry(int hash, K key, V value, Node<K,V> next) {
super(hash, key, value, next);
}
}
// 2. Adjust doubly linked list once a node is removed
void afterNodeRemoval(Node<K,V> e) { // unlink
LinkedHashMap.Entry<K,V> p =
(LinkedHashMap.Entry<K,V>)e, b = p.before, a = p.after;
p.before = p.after = null;
if (b == null)
head = a;
else
b.after = a;
if (a == null)
tail = b;
else
a.before = b;
}
// 2. Adjust doubly linked list once a node is added
void afterNodeInsertion(boolean evict) { // possibly remove eldest
LinkedHashMap.Entry<K,V> first;
if (evict && (first = head) != null && removeEldestEntry(first)) {
K key = first.key;
removeNode(hash(key), key, null, false, true);
}
}
// 3. If a node is replaced, move it to the end (its treated as newly added node)
void afterNodeAccess(Node<K,V> e) {
LinkedHashMap.Entry<K,V> last;
if (accessOrder && (last = tail) != e) {
LinkedHashMap.Entry<K,V> p =
(LinkedHashMap.Entry<K,V>)e, b = p.before, a = p.after;
p.after = null;
if (b == null)
head = a;
else
b.after = a;
if (a != null)
a.before = b;
else
last = b;
if (last == null)
head = p;
else {
p.before = last;
last.after = p;
}
tail = p;
++modCount;
}
}Skipped
- Iterators
- Serialization
- Red-Black Tree balancing
- Splitting the Tree
- EntrySet and Values methods
Conclusion
- For a core data structure being used billions (probably trillions) of times, its okay to introduce complexity to gain extra performance.
- There are always trade offs between performance and space overhead.
- Bitwise operators are performant and powerful.
- HashMap class has 2734 lines of code (& comments)!
- Seemingly simple looking operations can involve huge amount of code.
Cake and the cherry
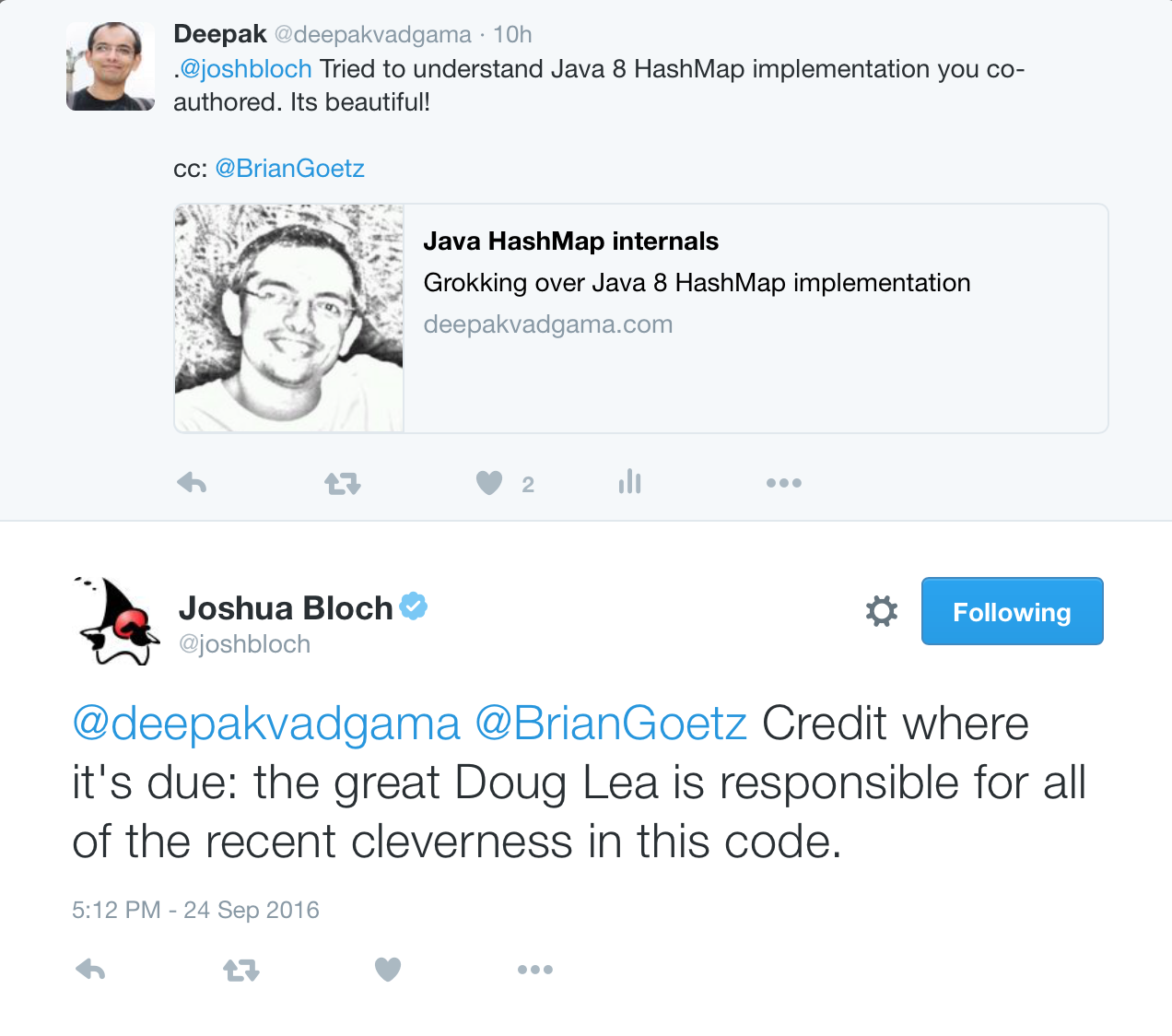
I got the following Twitter reply from Joshua Bloch which just made my day.
Goes to show the power of Twitter in democratizing communication (eg: between rockstar and average programmers) and also that programmer community at large is kind, helpful and generous.
Thanks: Special thanks to my friend Neerav Vadodaria for proof-reading the article.
Tags: java source-code-walkthrough
